1 感知机模型
感知机是一个简单的线性分类器。其定义为:假设输入空间是$\chi \subseteq R^n$,输出空间是$\gamma =\{+1, -1\}$.输入$x \in \chi$表示实例的特征向量,对应与输入空间的点;输出$y \in \gamma$表示实例的类别。由输入空间到输出空间的如下函数
称为感知机。其中$w和b$为感知机模型参数,$w \in R^n$叫做权值(weight)或权值向量(weight vector),$b \in R$叫做偏置(bias),$w \cdot x$ 表示$w$和$x$的内积。$sign$是符号函数,即
感知机有如下几何解释:线性方程
对应于特征空间$R^n$中的一个超平面$S$,其中$w$是超平面的法向量,$b$是超平面的截距。超平面$S$称为分离超平面。如图所示: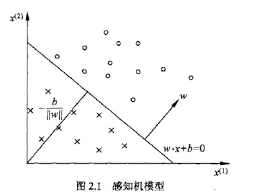
2 感知机学习策略
若一个数据集$T$存在一个超平面$S$可以将数据集中的所有正实例和负实例完全划分到超平面的两侧,那么可以说,数据集$T$是线性可分的,称为线性可分数据集。
误分类点$x_0$到超平面的距离为
,其中,$||w||$是$w$的$L_2$范数(向量各元素平方和的平方根)
所有误分类点到超平面$S$的总距离为
不考虑$\frac{1}{||w||}$,就可以得到感知机学习的损失函数。
给定训练数据集
其中,$x_i \in \chi = R^n, y_i \in \gamma = {+1, -1}, i = 1,2,…,N$.感知机$ sign(w \cdot x + b)$学习的损失函数定义为
其中$M$为误分类点的集合。一般误分类点离超平面越近,损失函数就越小。一个特定的损失函数:在误分类时是参数$w, b$的线性函数,在正确分类时是$0$.
3 感知机学习算法
感知机采用随机梯度下降法(stochastic gradient descent)来最小化损失函数。最小化过程是随机选取一个误分类点使其梯度下降。假设误分类点集合$M$是固定的,那么损失函数$L(w,b)$的梯度由
\begin{gather*}
\bigtriangledown_w L(w, b) = - \sum_{x_i \in M} y_i x_i \\
\bigtriangledown_b L(w, b) = - \sum_{x_i \in M} y_i
\end{gather*}
给出。
随机选取一个误分类点$(x_i,y_i)$,对$w$,$b$进行更新:
\begin{gather*}
w \leftarrow w + \eta y_i x_i \\
b \leftarrow b + \eta y_i
\end{gather*}
其中$\eta$是学习率,这样通过迭代可以期待损失函数$L(w,b)$不断减小,直到为$0$.
算法(感知机学习算法的原始形式)
输入:训练数据集$T={(x_1,y_1),(x_2,y_2),…,(x_N,y_N)}$,其中$x_i \in \chi = R^n, y_i \in \gamma = \{-1, +1\}, i = 1,2,…,N$;学习率$\eta(0< \eta \leq 1)$
输出:$w, b$;感知机模型$f(x)=sign(w \cdot x + b)$
(1)选取初值$w_0, b_0$
(2)训练集中选取数据$(x_i, y_i)$
(3)如果$yi(w \cdot x_i + b) \leq 0$
\begin{gather*}
w \leftarrow w + \eta y_i x_i \\
b \leftarrow b + \eta y_i
\end{gather*}
(4)转至(2),直至训练集中没有误分类点
其算法的最直观方式请看下图: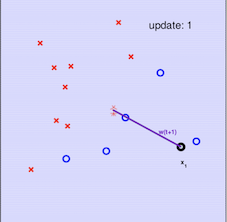
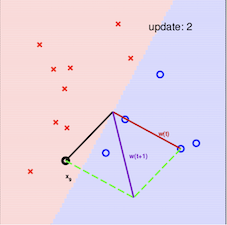
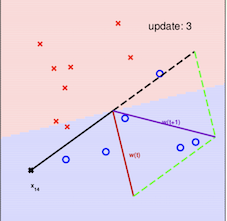
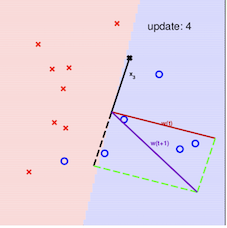
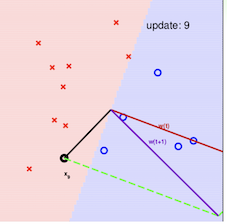
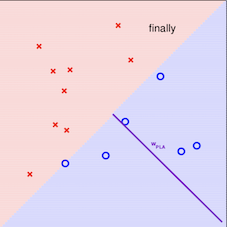
注意:在采用感知机算法中,选取误分类点的顺序不同,解可以不同
4 证明算法是收敛的

证明过程如下: